ფაილების კატალოგი

Paco Adajar conjecture

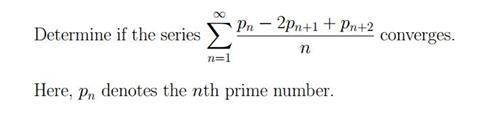
Emzari Papava: This series divergent or converges?

If a=p₁^k₁...p_n^k_n, a∈N, p_i∈P, i=1,2,3,...,n; Ndeg(a)=max{k₁,k₂,...,k_n} then Ndeg(ab)<=Ndeg(a)+Ndeg(b) but there exist Papava's open problem: Ndeg(a+b)<=?. Result: Many open problems in number theory. Prize: ,,Math King Rank".

Conjecture. If gcd(a,b)=1, d|(a+b) and (rad(d))³|d then d^1/2<rad(ab).

                   Emzar Papava

What is the probability that three points chosen at random on the circumference of a circle lie in one and the same semicircle? Equivalently, what is the probability that a random triangle inscribed in a circle has an obtuse angle?

PROVE: Evenly distributed in the circumference of the points. Let number points is 2n on the circumference then number of obtuse angle triangles is 2n(1+2+3+...+(n-2))=n(n-1)(n-2); number all triangls is (2n)!/(2n-3)!3!=2n(2n-1)(n-1)/3; 3n(n-1)(n-2)/2n(2n-1)(n-1)=3n(n-2)/2n(2n-1)→3/4 when n→∞ . Let number points is 2n+1 on the circumference then number of obtuse angle triangles is (2n+1)(1+2+3+...+(n-1))=n(n-1)(2n+1)/2; number all triangls is (2n+1)!/(2n-2)!3!=n(2n-1)(2n+1)/3; 3n(n-1)(2n+1)/2n(2n-1)(2n+1)=3n(n-1)/2n(2n-1)→3/4 when n→∞ .

Made in Georgia (Caucasus) by Emzari Papava

1/2+(1-1/2)/3+(1-1/2)(1-1/3)/5+(1-1/2)(1-1/3)(1-1/5)/7+(1-1/2)(1-1/3)(1-1/5)(1-1/7)/11+...=1

π(x)=...

card{(a,b,c): a,b,c€N; a+b>c, a+c>b, b+c>a; a<b<c<n}=n(n+2)(2n+5)/24  when n is even  number; 

card{(a,b,c): a,b,c€N; a+b>c, a+c>b, b+c>a; a<b<c<n}=(n+1)(n+3)(2n+1)/24  when n is odd number.

                            Emzari Papava